英文校正から自分の癖を知るシリーズ1
先日、あるオープンアクセス誌に英語論文を投稿しました。 後学のために、英文校正会社から返ってきた修正点のうち、自分がやらかしがちな部分を洗い出してみました。 同じような英語ライティングの癖を持っている人もいるかもしれないので、一般に公開してみることにします。基礎的なミスが多くて恥ずかしいですが...。 ちなみにイギリス英語の準拠して直してもらうようにオーダーしています。
基本的に過去形でいい
「(変数を)統制する」の意味でcontrolを使う時はforが必要
「日本の地方部で」はin rural area in Japanではなくin rural Japanで表せる
~was found to be...は単純にwasでよい
「に関する非対称性」のような時に使う「関する」はaboutではなくregarding
「観測できなかった」はcannot be observedではなくwas not observedでいい
APAの場合キーワードは頭文字が大文字
APAの場合ショートタイトルはすべて大文字。
It has been widely discussed that~は冗長
i.e.で言い換える時はカッコ内に書く
「~に対する偏見」はprejudice toではなくprejudice toward
「大きく依存する」はdeeply dependではなくdepends greatly
「~の黎明期」はat the early stage of~ではなくin the early stages of~
「~への調査」はresearch toではなくresearch on (surveyも同様)
「学部生」はungraduated studentsではなくundergraduate students
タイミング的に同時の場合はat the same timeではなくsimultaneously
「~を検討している研究」はstudies which examine...ではなくstudies examining...
もう一つ例を出す時はFor another exampleよりはIn another exampleのほうがベタ
examineとかevaluateだけじゃなくてassessも使えるようになりたい
長い文でも時制を保ちたい
electoronicではなくelectronic
「○○(学術用語)は~を表す」は~expresses...ではなくis an expression of...を使う
やたらとmean使わなくてもbe動詞でいい
settingsを使えるようになりたい
This studyの類義語としてThe current researchも使える
いろんな要素の間の違いを言う時はdifference amongではなくdifference across
いちいちtry to revealとか書かない。examineでいい。
色々列挙して他にも要素が考えられる場合はand moreで締める
In this perspectiveよりもFrom this perspectiveがベタ
「だけで引き起こされるわけではない」はbe not caused by only~ではなくbe not caused merely by~
「AとBは区別されなければならない」はmust be distinguished from one another
APAの場合、著者名にアクサンなどが入っていても本文中ではアルファベットで表記する
most famousよりもwell-knownのほうがこなれている
informationは不可算なのでthese informationとか言わない
「~を質問する」はaskじゃなくてask for
「後述の分析」はthe aforementhioned analysis
「~の問題に対応する」という意味ならto handle withじゃなくてto handleでいい
giveは口語なのでprovide等を使う
「~に同意する」なのにagree withを使わない。agree to。
「丸形の~」はround shapeではなくcircle shaped
読者の興味を引きたい時はEspeciallyではなくWorth noting,から始める
「言うなれば」の意味でnamely,を使いがちだが、要らない
対比を強調したい時はイタリック
「アルゴリズムを採用する」はemploy algorithm
「この研究にはいくつかの限界がある」はThere are some limitations to this study. on this studyではない。
「たった一例」ということを強調したければ単にaではなくa singleで形容する
APAの場合、編著本の中の章はページ数を(pp. 1-14)のようにppをつける
APAの場合、論文名は最初だけ大文字
RでERGMを実装したかった(が、失敗した)
このエントリは、Sansan Advent Calendar 2019 21日目の記事です。
- 基本的にタイトルの通りですが、この記事では統計的ネットワーク分析のデファクトスタンダードとなっているERGMをRで実装していきます。
- {igraph}以外のパッケージは使わずにできるだけスクラッチで開発します。
- 前もって断っておきますが、正しくパラメータ推定できるような実装には至ることができませんでした。
ERGMとは
- ERGM = Exponential Random Graph Model
- 日本語では「指数ランダムグラフモデル」と訳されることが多いです。
- 略称は「あーぐむ」と読むようです。
- 概要については以下の記事で紹介されています。
ERGMを使うと何が嬉しいのか
- 観測されたネットワークが、どのような構造的なメカニズムによって生成されたのかを知ることができます。
- ERGMの最大の強みは、ダイアド間の相互依存性を考慮できることにあります。
- ダイアドを1つのケースとして、エッジの有無を従属変数としたロジスティック回帰も可能ですが、これは残差の独立性の仮定に反してしまいます。
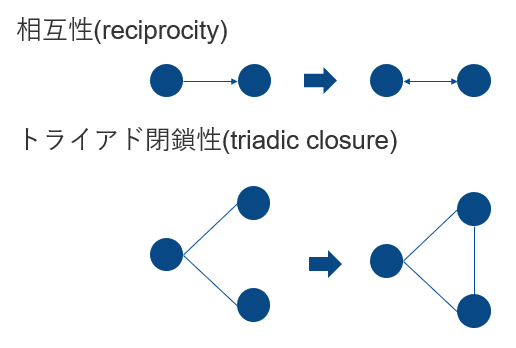
- 社会ネットワークにおいては、下の図のように、相互的なつながりが発生する傾向(相互性)や、友達同士は友達になりやすい傾向(トライアド閉鎖)がありますが、ERGMはダイアド同士の相互依存性を仮定できるので、このようなネットワーク内生的な効果を推定することができます。
- 例えば、トライアド閉鎖は、トライアングルの数などのネットワーク統計量をモデルに投入して、その効果を確認することができます。
- ERGMは一般に以下のような指数形式で定式化されます。
: ネットワークの確率変数。
: ネットワークの実現値(実際に観測されたネットワーク)。
: ネットワーク形象
のネットワーク統計量。
- 例えば、
に4つのトライアングルが含まれている場合、
。
- 例えば、
: ネットワーク形象
に対応するパラメータ。
:モデル内で検討するトライアングルなどのネットワーク形象の集合。
: 正規化定数。可能なすべてのネットワークの
の合計値。
- N=20ほどの小規模ネットワークでも現実的に計算できない数の膨大なネットワークを検討しなければならないため、
の計算を回避するためのテクニックが色々と考案されています。
- N=20ほどの小規模ネットワークでも現実的に計算できない数の膨大なネットワークを検討しなければならないため、
例えば、ERGMで以下のようにパラメータが推定されたとします。
Pr=exp(-0.5*エッジ数+0.5*閉鎖トライアドの数+0.2*同じ性別間のつながりの数)
この時、観測されたネットワークにおいて「友達同士が友達になりやすい」(トライアド閉鎖)という傾向と「同じ性別同士でつながりやすい」(ホモフィリー)という傾向が同時に作用していると解釈することができます。
ERGMを用いた研究事例は色々あるのですが、Goodreau et al. (2009)は、アメリカの学校内でのホモフィリーを、トライアド閉鎖の効果を統制しながら推定しています。
- ここからは、{ergm}パッケージを用いたERGMの推定と、RによるERGMパラメータ推定の実装の一例について紹介します。
セッション情報
- RStudio Cloud上で動かしています。
> sessionInfo() R version 3.5.3 (2019-03-11) Platform: x86_64-pc-linux-gnu (64-bit) Running under: Ubuntu 16.04.6 LTS Matrix products: default BLAS: /usr/lib/atlas-base/atlas/libblas.so.3.0 LAPACK: /usr/lib/atlas-base/atlas/liblapack.so.3.0 locale: [1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8 LC_COLLATE=C.UTF-8 LC_MONETARY=C.UTF-8 [6] LC_MESSAGES=C.UTF-8 LC_PAPER=C.UTF-8 LC_NAME=C LC_ADDRESS=C LC_TELEPHONE=C [11] LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C attached base packages: [1] stats graphics grDevices utils datasets methods base other attached packages: [1] coda_0.19-2 forcats_0.3.0 stringr_1.3.1 dplyr_0.8.3 purrr_0.3.3 [6] readr_1.3.1 tidyr_0.8.2 tibble_2.1.3 ggplot2_3.1.0 tidyverse_1.2.1 [11] igraph_1.2.4.1 statnet_2019.6 tsna_0.3.0 sna_2.4 ergm.count_3.3.0 [16] statnet.common_4.3.0 tergm_3.6.1 networkDynamic_0.10.0 ergm_3.10.4 network_1.15
{ergm}の使い方
- アメリカ西海岸のネットワーク分析の研究者らが中心となって開発されているパッケージです。
- 社会ネットワーク分析用の{sna}やネットワークオブジェクトを管理する{network}などが全部入りの{statnet}というパッケージスイートがあり、こちらを導入するのが便利です。
> library(statnet) statnet: version 2019.6, created on 2019-06-13 Copyright (c) 2019, Mark S. Handcock, University of California -- Los Angeles David R. Hunter, Penn State University Carter T. Butts, University of California -- Irvine Steven M. Goodreau, University of Washington Pavel N. Krivitsky, University of Wollongong Skye Bender-deMoll Martina Morris, University of Washington Based on "statnet" project software (statnet.org). For license and citation information see statnet.org/attribution or type citation("statnet").
- 今回は、メディチ家の婚姻ネットワークデータ
flomarriageを用います。 - とりあえず
plotしてみます。
data(florentine) plot(flomarriage)
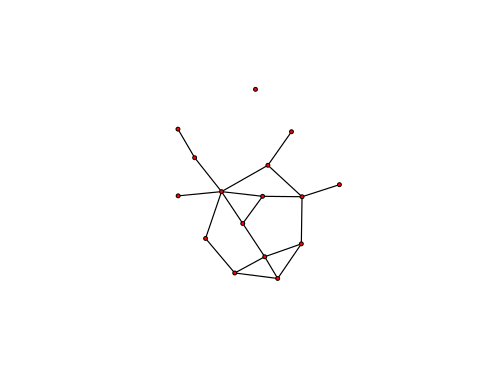
- ネットワーク統計量は
summary()関数を使うと計算できます。- 今回は、エッジの本数(edges)とトライアングル(triangle)に着目します。
> summary(flomarriage ~ edges + triangle) edges triangle 20 3
- これらのネットワーク統計量からなるモデルを構築し、ERGMのパラメータを推定してみます。
> ergm_model <- ergm(flomarriage ~ edges + triangle) Starting maximum pseudolikelihood estimation (MPLE): Evaluating the predictor and response matrix. Maximizing the pseudolikelihood. Finished MPLE. Starting Monte Carlo maximum likelihood estimation (MCMLE): Iteration 1 of at most 20: Optimizing with step length 1. The log-likelihood improved by 0.003736. Step length converged once. Increasing MCMC sample size. Iteration 2 of at most 20: Optimizing with step length 1. The log-likelihood improved by 0.0002205. Step length converged twice. Stopping. Finished MCMLE. Evaluating log-likelihood at the estimate. Using 20 bridges: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 . This model was fit using MCMC. To examine model diagnostics and check for degeneracy, use the mcmc.diagnostics() function.
- 結果を確認してみます。通常の
lmと同じく、summary()関数で推定結果の詳細を確認できます。
>summary(ergm_model) ========================== Summary of model fit ========================== Formula: flomarriage ~ edges + triangle Iterations: 2 out of 20 Monte Carlo MLE Results: Estimate Std. Error MCMC % z value Pr(>|z|) edges -1.6743 0.3488 0 -4.801 <1e-04 *** triangle 0.1626 0.5894 0 0.276 0.783 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Null Deviance: 166.4 on 120 degrees of freedom Residual Deviance: 108.1 on 118 degrees of freedom AIC: 112.1 BIC: 117.6 (Smaller is better.)
実装編
- さて、続いてはRでできるだけゼロからERGMを実装することを試みます。
下準備
- flomarriageは
networkオブジェクトなので、igraphオブジェクトに変換します。- {intergraph} を用いると、この作業が非常に簡単になります。
library(igraph) library(intergraph) g <- intergraph::asIgraph(flomarriage) plot(g)
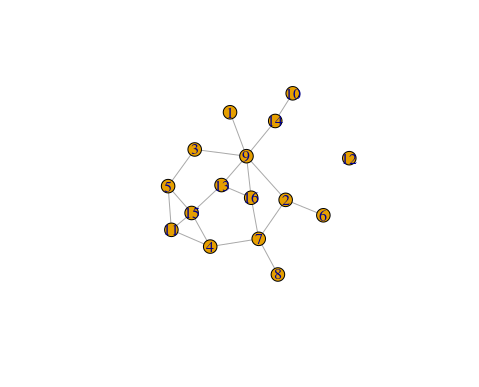
ネットワーク統計量を計算する関数
- 本当は行列計算でも書けるのですが…
#エッジの数 count_edges <- function(g){ edges <- length(E(g)) return(edges) } #トライアングルの数 count_triangle <- function(g){ triangle <- motifs(g)[4] if(is.na(triangle)){ triangle <- 0 } return(triangle) }
- 先ほどの結果と一致します。
> count_edges(g) [1] 20 > count_triangle(g) [1] 3
推定のステップ
- ERGMのパラメータ推定は以下のステップで行われます。
(1) 疑似尤度最大化(MPLE)による の決定
(2) MCMCによるランダムグラフ生成
(3) (2)で得られたサンプルを用いた対数尤度比の最大化 -> の推定
- (2),(3)のステップはモンテカルロ尤度最大化(MC-MLE)と呼ばれています。
- 少しトリッキーになりますが、MC-MLEの説明から始めます。
変化統計量
- MC-MLE自体の説明に入る前に、まず、変化統計量について説明します。
- 他のすべてのダイアドの状態
を一定として、ダイアド
の状態を変化させた時の、ネットワーク統計量の変化を 変化統計量(change statistics)と呼びます。
MCMCによるランダムグラフ生成
- ある固定された
のもとで、変化統計量の比 [\pi] を計算します。
を上手く決めれば、観測されたネットワークに近いようなランダムグラフが生成されていきます。
を遷移確率として、次のサンプルに進みます。こうしてランダムグラフのサンプルを生成していきます。
##ダイアドの状態をスイッチさせる change_edge <- function(graph,i,j){ if(graph[i,j] == 1){ graph[i,j] <- 0 }else{ graph[i,j] <- 1 } return(graph) } ##ランダムにダイアドの状態をスイッチさせたグラフを返す random_propose <- function(graph){ sampled_pairs <- sample(1:length(V(graph)),2,replace = FALSE) i <- sampled_pairs[1] j <- sampled_pairs[2] graph <- change_edge(graph,i,j) return(graph) }
MC-MLE
metropolis <- function(graph, theta0_edges, theta0_triangle){ ##現在のネットワーク current_graph <- graph current_edges <- count_edges(current_graph) current_triangle <- count_triangle(current_graph) ##提案されたネットワーク proposed_graph <- random_propose(graph) proposed_edges <- count_edges(proposed_graph) proposed_triangle <- count_triangle(proposed_graph) ##変化統計量の計算 changed_edges <- proposed_edges - current_edges changed_triangle <- proposed_triangle - current_triangle ##piを計算し、提案されたグラフを採択するかどうか決める change_ratio <- exp(theta0_edges*changed_edges + theta0_triangle*changed_triangle) move_probability <- min(1,change_ratio) if(move_probability >= runif(1)){ return(proposed_graph) }else{ return(current_graph) } }
- MCMCの実装
MCMC <- function(graph, burn_in = 10000, samplesize = 50000, theta0_edges = 0.1, theta0_triangle = 0.1){ graph <- graph.empty(length(V(graph)),directed=FALSE) edges_c <- count_edges(graph) triangle_c <- count_triangle(graph) par(mfrow = c(2,2)) for(i in 1:samplesize){ if(i %% 1000 == 0){ progress_text <- paste0(i,"(",round(100*(i/samplesize),3),"%) done") print(progress_text) plot(edges_c,type="l") hist(edges_c) plot(triangle_c,type="l") hist(triangle_c) } after_graph <- metropolis(graph,theta0_edges,theta0_triangle) edges_c <- c(edges_c,count_edges(after_graph)) triangle_c <- c(triangle_c,count_triangle(after_graph)) graph <- after_graph } return(list(edges = edges_c[(burn_in+1):samplesize], triangle = triangle_c[(burn_in+1):samplesize],obs_graph = graph)) }
MPLE
- さて、ここまでMCMCを用いたランダムグラフの生成は
を前提としていましたが、この値自体はどのように決めればいいのでしょうか。
- 実は、
は
の真値に近くないと、正しい分布からランダムグラフを生成してくれないという問題があるため、できるだけ近い値を
としたいです。
- そこで、疑似尤度の最大化(Maximum Pseudo-Likelihood Estimation, MPLE)で推定されたパラメータを
とします。
- これは、ダイアド同士の統計的連関を考慮しないモデル (dyad-independence) と同値であり、構造的特徴のないモデルではMCMCを行わず、MPLEのみが使われます。
- これは非常にシンプルで、観測されたネットワークのダイアドにおけるエッジの有無を、ネットワーク統計量の変化統計量で回帰するロジスティック回帰を行うことで達成されます。
#変化統計量とエッジの存在からなるデータフレームを生成 generate_changed_data <- function(graph){ changed_data <- data.frame() for(i in 1:length(V(graph))){ for(j in 1:length(V(graph))){ if(i >= j){ next } existing_if <- graph[i,j] changed_graph <- change_edge(graph,i,j) changed_triangle <- abs(count_triangle(changed_graph) - count_triangle(graph)) row <- data.frame(i = i, j = j, existing_if = existing_if, changed_triangle = changed_triangle) changed_data <- rbind(changed_data,row) } } return(changed_data) } #MPLEの実装 MPLE <- function(graph){ data_for_mple <- generate_changed_data(graph) reg <- glm(data = data_for_mple, existing_if ~ changed_triangle, family = "binomial") return(list(edges = reg$coefficients["(Intercept)"], triangle = reg$coefficients["changed_triangle"])) }
- MPLE -> MC-MLEまでのプロセス
## SAMPLING triangle_model <- function(graph, burn_in = 10000, samplesize = 50000){ message("Starting MPLE fitting...") theta0_list <- MPLE(graph) print(theta0_list) message("MPLE fitting done. Now starting MC-MLE fitting...") fit <- MCMC(graph, burn_in = burn_in, samplesize = samplesize, theta0_edges = theta0_list$edges, theta0_triangle = theta0_list$triangle) fit$theta0_edges <- theta0_list$edges fit$theta0_triangle <- theta0_list$triangle return(fit) }
- 実際にMCMCからネットワーク統計量のサンプルを得ます。
fit <- triangle_model(g, burn_in = 10000, samplesize = 50000)
対数尤度比の最大化
- さて、MCMCからネットワーク統計量のサンプルが得られました。次はこれを用いて、実際にパラメータを推定していきます。
- 尤度それ自体は正規化定数を計算しなければ最大化できないので、代わりに、ある固定された
を用いた
=対数尤度比の最大化を目指します。
は、以下のように近似できます。
#対数尤度比を計算する関数 loglikelihood_ratio <- function(theta,fit,n){ sample_length <- length(fit$edges) sample_index <- (sample_length-n):sample_length sampled_edge_count <- fit$edges[sample_index] sampled_triangle_count <- fit$triangle[sample_index] theta0 <- c(fit$theta0_edges,fit$theta0_triangle) g_obs <- c(count_edges(fit$obs_graph),count_triangle(fit$obs_graph)) first = (theta - theta0) %*% g_obs exp_vec <- c() for(i in 1:n){ sam <- exp((theta - theta0) %*% c(sampled_edge_count[i],sampled_triangle_count[i])) exp_vec <- c(exp_vec,sam) } second <- log(sum(exp_vec)/length(exp_vec)) loglikelihood_ratio <- first - second return(loglikelihood_ratio) }
optim()関数を使って、MCMCで得られたグラフのネットワーク特徴を与えて、対数尤度比を最大化してみます。
##対数尤度比の最大化 my_estimates <- optim(par = c(0,0), #初期値 fn = loglikelihood_ratio, #目的関数 control = list(fnscale=-1), #最大化するため fit = fit, n = 1000) #MCMCサンプルサイズ
- さて、いよいよオレオレERGMの推定結果を確認します。
- {ergm}で求めたパラメータと比べてみます。
> ergm_model$coef #推定結果 ({ergm}) edges triangle -1.674332 0.162630 > my_estimates$par #推定結果 (オレオレergm) [1] -1.8267176 0.2983575
- それなりに近い推定値にはなっているものの、ややズレてしまっています。
問題:MCMCが上手くランダムグラフを生成していない
- 当初は最適化関数の扱いに問題があるのかと思い、初期値などを色々試してみるも無駄に終わってしまいました。
- 調べてみると、MCMCが上手くランダムグラフを生成していまいことがわかりました。
- まず、{ergm}を用いて生成したmcmcsampleは以下のようなtraceplotを呈します。
- わかりやすくするために、観測されたグラフのネットワーク統計量が0になるようにセンタリングしています。
> mcmc.diagnostics(ergm_model, esteq = FALSE, center = TRUE)
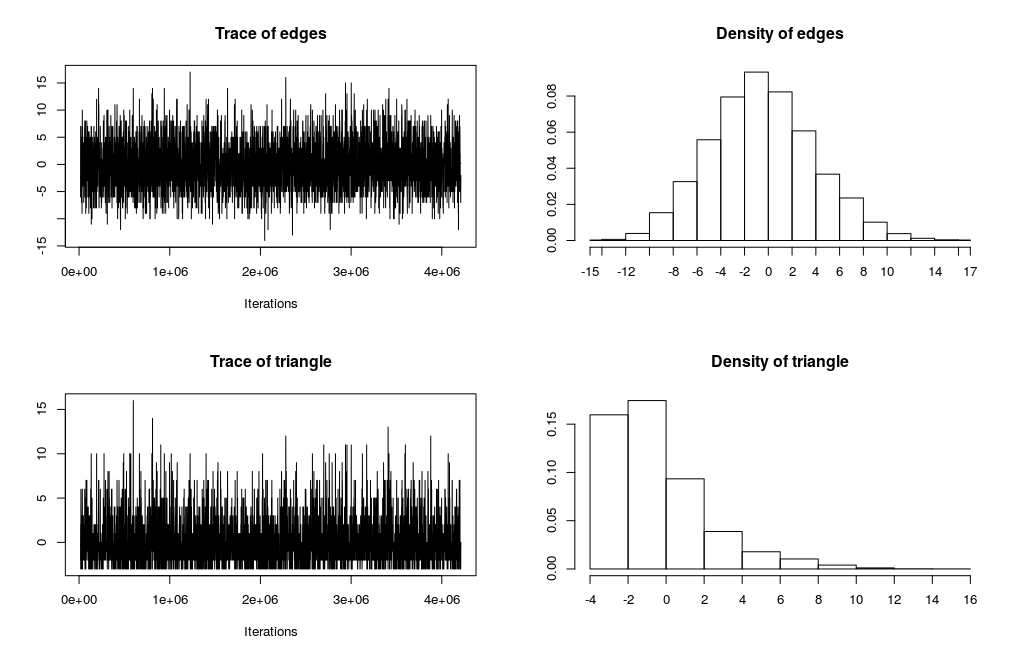
- 一方、自分で実装したmcmcsampleを見てみます。
ergm::mcmc.diagnostics()と似たプロットを行う関数を作ります。
##オレオレMCMCのサンプル生成結果をplot diagnosis <- function(fit){ edges_c <- fit$edges triangle_c <- fit$triangle obs_edges <- count_edges(fit$obs_graph) obs_triangle <- count_triangle(fit$obs_graph) edges_centered <- edges_c - obs_edges triangle_centered <- triangle_c - obs_triangle par(mfrow = c(2,2)) plot(edges_centered,type="l",) hist(edges_centered) plot(triangle_centered,type="l") hist(triangle_centered) }
- 結果がこちらです。
> diagnosis(fit)
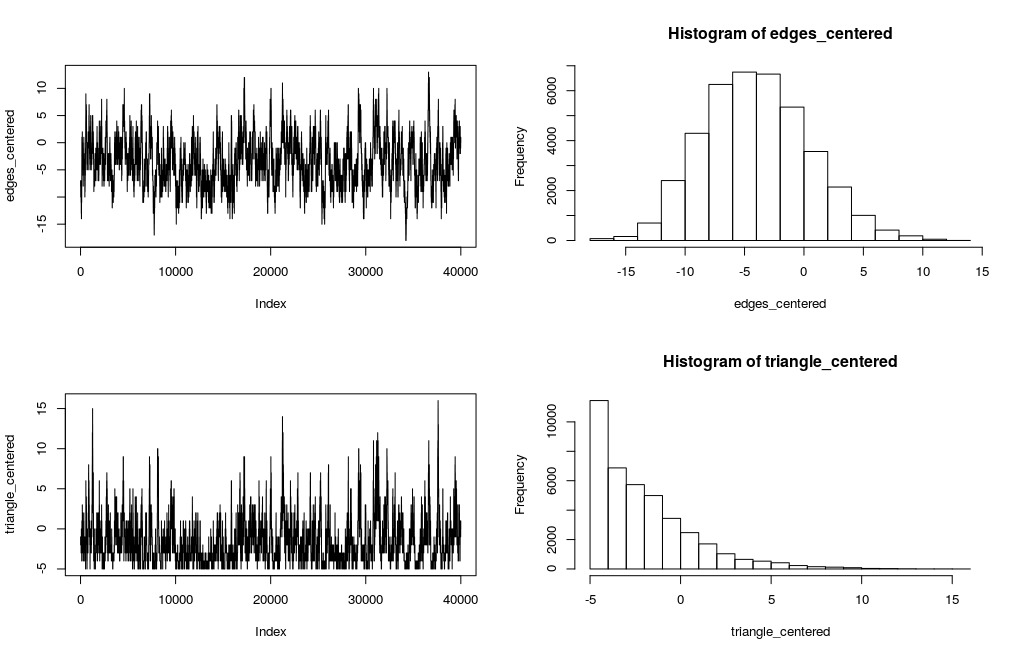
- 観測値に比べるとマイナス側に偏った分布になってしまっています。
さいごに
- 今回は時間が足りず、これ以上のことはできませんでした。
- 尻切れトンボにようになってしまいますが、なぜ上手く推定できないのかも含めて、この課題に引き続き取り組んでいこうと思います。
参考文献
- Garry RobinsらによるERGMの総説論文:An introduction to exponential random graph (p*) models for social networks - ScienceDirect
- ERGMの推定法に関するコンパクトなまとめ:Archive ouverte HAL - Introduction to network modeling using Exponential Random Graph models (ERGM)
- statnetチームによる過去のワークショップ資料:https://statnet.org/trac/wiki/WorkshopArchive
- 推定に関して一番わかりやすいのはHunterによる2006年のEstimationの資料
- ERGMs with Rhttps://acaimo.github.io/SNAR_BOOK/MLE-ERGMs.html#monte-carlo-maximum-likelihood-estimation-mc-mle
{parallelDist}が鬼速い
R Advent Calendar 2019 15日目の記事です。
タイトルだけで内容の99%は伝わっていると思うのですが、{parallelDist} ライブラリが並列でベクトル間の距離計算をしてくれて、鬼のように速いという話をします。
締め切り前なのに距離計算が間に合わない!という時に重宝します。
Dynamic Time Warpingとは
- 今回はDynamic Time Warpingという距離を例にparallelDistの威力を紹介します。
- 時系列シーケンス間の距離。時系列クラスタリングによく用いられる。
- 平行移動や長さ・周期の違いに対してロバストな類似度を計算できる。
- 先人による解説:
- 一方で計算量がとても大きい。
- 2つのシーケンスを総当りで計算するので、長さnの系列と長さmの系列のDTW距離を計算しようとするとO(nm)かかる。
セッション情報
- WSL上で動かしています。
sessionInfo()
R version 3.4.4 (2018-03-15) Platform: x86_64-pc-linux-gnu (64-bit) Running under: Ubuntu 18.04.2 LTS Matrix products: default BLAS: /usr/lib/x86_64-linux-gnu/blas/libblas.so.3.7.1 LAPACK: /usr/lib/x86_64-linux-gnu/lapack/liblapack.so.3.7.1 locale: [1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8 [4] LC_COLLATE=C.UTF-8 LC_MONETARY=C.UTF-8 LC_MESSAGES=C.UTF-8 [7] LC_PAPER=C.UTF-8 LC_NAME=C LC_ADDRESS=C [10] LC_TELEPHONE=C LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C attached base packages: [1] stats graphics grDevices utils datasets methods base
パッケージインストール
install.packages("TSclust") install.packages("dtw") install.packages("parallelDist")
ライブラリ読み込み
library(magrittr) library(dplyr) library(tidyr) library(purrr)
ランダムウォークによる系列の生成
random_walk <- function(x,t){ return(cumsum(rnorm(t))) } set.seed(1024) series_data <- map_dfc(1:100,random_walk,t=100) #この記法は重宝しますね
plot_data <- series_data %>% mutate(period = row_number()) %>% gather(key = series, value = value,-period) g <- ggplot(plot_data,aes(x = period, y = value, group = series)) g <- g + geom_line(stat="identity") g

{TSclust}を使う
- DTWを計算する時に一番多く使われているのはこのパッケージかと思います。
- 先人による解説:
tsclust_time <- system.time({ tsclust_dist <- TSclust::diss(series_data,"DTWARP") }) tsclust_time["user.self"]
user.self
19.609
{dtw}を使う
- 距離の正規化の手法などが充実した、柔軟なライブラリ
- ドキュメンテーション:http://dtw.r-forge.r-project.org/
dtw_time <- system.time({ dtw_dist <- dtw::dtwDist(t(series_data)) #dtwの場合は時系列を行として配置 }) dtw_time["user.self"]
user.self
22.141
parallelDistを使う
- とにかく鬼速く距離計算してくれるライブラリ
- 何故速いのか?
RcppParallelによるマルチスレッド計算RcppArmadilloによる行列計算の最適化- CRTPによる仮想関数の回避(よくわからない…)
- GitHub : https://github.com/alexeckert/parallelDist
pardist_time <- system.time({ pardist_dist <- parallelDist::parDist(t(series_data), method = "dtw", step.pattern="symmetric2") #dtwのデフォルトと合わせる }) pardist_time["user.self"]
user.self
2.922
- お、鬼速い…((((;゚Д゚))))
- 約7倍の速度向上。
結果は同じ?
- どのライブラリでも結果は同じなのか恐る恐る確認してみる。
as.matrix(tsclust_dist)[1:10] as.matrix(dtw_dist)[1:10] as.matrix(pardist_dist)[1:10]
[1] 0.0000 399.4580 207.6915 150.0798 733.7981 2201.4722 345.4040 [8] 1569.0761 1201.3074 415.9536 [1] 0.0000 399.4580 207.6915 150.0798 733.7981 2201.4722 345.4040 [8] 1569.0761 1201.3074 415.9536 [1] 0.0000 399.4580 207.6915 150.0798 733.7981 2201.4722 345.4040 [8] 1569.0761 1201.3074 415.9536
階層的クラスタリング
- せっかくなので階層的クラスタリングも高速な {fastcluster}パッケージを使う。
hc <- fastcluster::hclust(pardist_dist) plot(hc) trees <- cutree(hc,3)

クラスタリング結果の可視化
cluster_data <- tibble(series = names(trees), cluster = as.factor(trees)) plot_data <- series_data %>% mutate(period = row_number()) %>% gather(key = series, value = value,-period) %>% left_join(cluster_data,by="series") g <- ggplot(plot_data,aes(x = period, y = value, group = series, col = cluster)) g <- g + geom_line(stat="identity") g

- 時点数Tと系列数Nと、{dtw}比の計算時間の関係を検証したかったのですが、時間とマシンスペックが足りず…。
- 暇な時にやろうかと思います。
補足
- {TSclust}が依存している{rgl}を入れる時に
unable to open X11 displayと怒られたが、Sys.setenv("RGL_USE_NULL"=TRUE)で解決した。
朝型人間に擬態するためにやっていること
親譲りでない夜型人間で小供の時から損ばかりしている。
―― 夏目漱石『夜型人間ちゃん』
夜型人間 Advent Calendar 2019 1日目の記事です。
2年ほど前にフルタイムワーカーを始めてからというもの、自分なりに色々と試行錯誤しながら、朝型人間に「擬態」する術を身につけてきました。
自分は根っからの「夜型人間」だと自認しており、修士課程の時に概日リズムをぶっ壊してからも、いまだに朝は自分の時間ではないと思っています。作業が捗り、良いアイデアが降ってくるのは大抵22時以降です。
最近、「夜型か朝型かはゲノムレベルで規定されており、この違いを努力でカバーすることは困難である」という趣旨の記事が話題になりました。この知見に関する妥当性は、専門外のため保留させていただきますが、「朝型人間と夜型人間の共存」についての議論のきっかけになることを願っています。
しかし、規範や制度が急速に変わることは稀です。生活リズムというテーマに関しても、明日いきなり社会の寛容度が向上することは、おそらく見込めないでしょう。さしあたり個人の幸福にとって重要なのは、「どうすれば朝型の社会をやり過ごすことができるか」です。この記事では、「環境構築」を中心に、自分が朝型人間に「擬態」するために導入したガジェットや、普段実践している生活習慣を紹介します。
といっても、人類はみな朝型人間か夜型人間のどちらかというわけではなく、両極の間のスペクトラムだとは思いますし、僕以上に深刻な夜型の方もいらっしゃることでしょう。場合によっては、医療機関への相談のほうが近道かもしれません。
それに、僕自身がこの記事で紹介することを実践しながらも少なくとも月に1,2回「やらかして」いるので、話半分に読んでいただけると幸いです。専門的な見地からみて間違っていることがあればご指摘ください。
この記事を通して、「いつも遅刻してくるあいつ」も実は頑張っているかもしれないですよ、ということが伝えられたらよいと思っています。
環境構築
朝型人間への擬態をする上での僕の基本戦略は「環境の改変」です。夜型人間なら誰しも、朝に起きたいと思っても起きられない朝をいくつも経験したことでしょう。眠る前の自分はあまりに楽天家で、寝覚めの瞬間の自分は、私たちが想像するよりも遥かに狡猾です。自分の意思ほど信頼できないものはありません。
環境の中には、寝具や耳栓のように入眠確率を上げる類のものと、目覚ましのように起床確率を上げる類のものがあると思っています。
寝具
博士課程に入りたての頃、祈るようにしてマニフレックスのマットレスと枕を購入しました。当時としてはかなり思い切った判断でした。東急ハンズの寝具売り場を足繁く通っていた記憶があります。長い間すのこベッドに薄い敷ふとんを敷いて寝ていたのですが、睡眠環境は見違えるように変化しました。マットレスも枕も肉厚なため、体重85kg超えの自分でも底に身体が当たることはなく、非常に快適です。他のメーカーも試しましたが、最終的には厚みで選んだ形です。この投資は非常に効果があり、「なんか固くて寝にくいな…」という入眠時の思考のノイズを減らせた気がします。

- 出版社/メーカー: Magniflex(マニフレックス)
- メディア: ホーム&キッチン
- この商品を含むブログを見る

マニフレックス 三つ折り マットレス 高反発 メッシュ・ウィング ミッドブルー シングル【10年保証】【外して洗える側地】※コンパクトなロール圧縮梱包
- 出版社/メーカー: Magniflex(マニフレックス)
- メディア: ホーム&キッチン
- この商品を含むブログを見る
最近は、パラマウントベッドが販売しているActive Sleepというベッド+マットレスが気になっていますが、いかんせん高価なので手が出ませんね…。
耳栓
耳栓も、入眠確率を上げるための重要なツールです。僕は人の声や環境音が気になって眠れなくなるタイプなので、耳栓はほぼ必須です。AmazonでMOLDEXの耳栓が200ペアまとめ買いできるので、これを定期的に購入しています。
耳栓をすると目覚ましの音が聞こえないのではないかと思われるかもしれませんが、自分の場合は寝返りのせいか、朝起きたときには外れていることが多く、そこまで起床の妨げにはなっていません。もちろん個人差あり、起床確率が下がる方向に作用する方もいらっしゃると思うので、注意してください。

MOLDEX モルデックス カモフラ迷彩色耳栓 6608 コード無し 200ペア
- 出版社/メーカー: MOLDEX
- メディア: その他
- この商品を含むブログを見る
目覚まし
続いては起床確率を上げるための目覚ましシステムです。普段使いしているのは5つです。音・光・振動の感覚複合的なアプローチを採用しています。
デジタル目覚まし時計
- 普通のデジタル時計です。もう10年くらい使っていますね。
スマートフォンのアラーム
- LGV30+デフォルトのアラームアプリです。
旧スマホのSleepCycle
- マイクで睡眠中の寝返りの音などを拾って、睡眠の浅い時に起こしてくれるアプリです。
- これを導入してからは本当に高確率で起きられるようになりました。
- 過去の睡眠の傾向を分析してくれるアナリティクス機能(有料)は使用していません。
- 簡易的な光目覚まし

- 出版社/メーカー: スイッチボット(SwitchBot)
- メディア: Tools & Hardware
- この商品を含むブログを見る

Nature スマートリモコン Nature Remo mini Remo-2W1
- 出版社/メーカー: Nature 株式会社
- メディア: エレクトロニクス
- この商品を含むブログを見る

- 出版社/メーカー: フィリップスライティング(Philips Lighting)
- 発売日: 2017/11/06
- メディア: ホーム&キッチン
- この商品を含むブログを見る
- HuaweiBand
- スマートウォッチの一種です、アラーム機能が優秀です。
- 寝返りを記録して、睡眠の浅い時にバイブレーションで起こしてくれます。
- Apple WatchやFitBitでも同様の機能があるかと思います。

HUAWEI Band 3 Pro 0.95インチスマートウォッチ ブラックGPS内蔵 5気圧耐水 iOS/Android対応 Band 3 Pro/Black 【日本正規代理店品】
- 出版社/メーカー: HUAWEI(ファーウェイ)
- 発売日: 2018/10/19
- メディア: エレクトロニクス
- この商品を含むブログを見る
- その他
生活習慣
環境の改変ではないですが、普段の生活習慣については、該日リズムを壊した時に医者から勧められたことを実践し続けています。つくづく「入眠・起床の確率を上げるための戦いは、日中から既に始まっている」ということに尽きます。
- 19時以降にカフェインを摂取しない。お茶も飲まない。
- カフェインの半減期は4-6時間のようです。24時過ぎに就寝することを目標としているので、そこから逆算しています。
- 23時を過ぎたらPCを見ない。
運動する
休日に寝溜めをしない。
- こればっかりは環境でどうこうできる問題ではないような気もしますが、休日の朝に楽しい予定を入れておくと、リズムが保ちやすいのではないかと思っています。何より、寝すぎると偏頭痛がつらいです。
- 自分の場合は最近マイブームの水族館や野鳥撮影が大きなインセンティブになっています。
- 大型連休は、睡眠リズムが壊れやすいので天敵です…。
- こればっかりは環境でどうこうできる問題ではないような気もしますが、休日の朝に楽しい予定を入れておくと、リズムが保ちやすいのではないかと思っています。何より、寝すぎると偏頭痛がつらいです。
以上、根っからの夜型人間の僕が朝型人間に擬態するためにやっていることを紹介してきました。 前述したとおり、これだけやってもうまく眠れなかったり朝起きられないこともありますが、「なんとかやれる」水準まで持って行けている気がしています。毎日、夜に眠気が来るとホッとします。
皆さまの朝型人間への擬態も、うまくいくようにお祈りしています。
"Thanks God I'm Falling asleep!"
一般化Freeman指数の計算
はじめに:Freeman指数とは
Freeman指数は社会ネットワークにおけるセグリゲーションの程度を評価するための指標であり、とりわけエッジが対称化された無向ネットワークに対して用いられる。Freeman(1978)によって提案された。
この指数を使用している研究事例としては、例えば、学年によってエスニシティとジェンダーに関するセグリゲーションの程度を比較したShrum et al (1988)等が挙げられる。
基本的な発想は、「ランダムに紐帯が生成された時と比較して、観測されたネットワークにおいてグループを横断する紐帯がどれほど少ないと言えるか」によってセグリゲーションを測るというものである。Freeman指数は0から1までの値を取り、1に近いほど、グループ間のつながりが期待値と比べて少ないことになる。
しかしながら、Freeman(1978)で提出されたオリジナルの指数は、カテゴリを2つのみ持つ社会的次元(e.g. 「男性」と「女性」)でしか使用できないという問題がある。検討したい社会的次元が、「野球部」「サッカー部」「テニス部」のような3つ以上の幅広いカテゴリを持つ場合、この指数はこのままでは使うことができない。
一般化Freeman指数
Bojanowski and Corten(2014)は、Freeman指数を3つ以上の社会的カテゴリを含む社会的次元に関するセグリゲーションに対しても適用できるように改良した一般化Freeman指数(Generalized Freeman’s Index)を開発している.
下式は一般化Freeman指数を定式化したものである.なお,詳しい導出の過程は元論文を参照されたい.
ここでπは,観測されたネットワークと同じノードの集合を所与とし、紐帯が完全にランダムに生成された仮定した時に発生するグループ間紐帯の全体に占める割合を示し,pは,実際に観測されたネットワークが含むグループ間紐帯の割合を,Nは全てのノード数を,n_kはグループkを構成するノードの数を示している.通常のFreeman指数と異なり、グループ数が多すぎる場合は Sが0を下回る場合もある。
実装
簡単に実装してみたのが以下のコード。属性付きの network オブジェクトを引数に取る。どの属性でFreeman指数を計算するかは、引数 mode で指定する。
igraph オブジェクトが使いたい場合は、 intergraph::asIgraph() などで変換すると良い。
library(network) Freeman <- function(network,mode){ matrix <- mixingmatrix(network,mode)$matrix #混合行列(属性間のエッジ数を成分とする行列) matrix[upper.tri(matrix)] <- 0 #ダブルカウントになるので上三角成分を0に N <- network.size(network) #ノード数 attribute <- network %v% mode #所望の属性をvectorで取得 nk_sum_sq <- N^2 nk_sq_sum <- sum(table(attribute)^2) sum_of_mgh <- sum(matrix) - sum(diag(matrix)) #異なるグループ間のエッジ数 p <- sum_of_mgh / sum(matrix) #異なるグループ間のエッジの割合(観測値) freeman <- 1 - p*N*(N-1)/(nk_sum_sq - nk_sq_sum) return(freeman) }
例
Freeman(net, mode = "gender")
注意点
ここで注意しなければならないのは,確かにFreeman指数を用いることでそれぞれ社会的次元に関して発生するセグリゲーションの度合いを個々に評価することはできるが,異なる社会的次元同士の関連(例えばジェンダーと所属部活の関連)や,構造的な紐帯形成プロセス(transitive closureなど)を考慮に入れられないということである。そのような場合は、ERGMなどの多変量解析の手法を用いるのがよい。
何もかも忘れて浮間公園に行く
最近は現実がつらすぎるので、公園で探鳥ばかりしている。
先週、板橋区の都立浮間公園に足を運んだので記録を残しておく。
↓東京都公園協会のページ www.tokyo-park.or.jp
午前7時30分頃。JR埼京線の浮間舟渡駅を降りると、すぐ目の前が公園。

入り口の広場では、ハトの大群が日光浴を楽しんでいた。

「浮間ヶ池」という名の大きな池を囲むようにして遊歩道が整備されていた。
この日池にいたのはカルガモ、カイツブリ、そしてゴイサギ。 ※クロップしまくってるので画質が粗い
写真こそ撮影していないものの、ツバメの群れもいた。



ゴイサギを生で見たのは初めて。今月の月刊BIRDERによればこの20年間で分布が半減したらしい。
公園の奥の方は柵で囲われたバードサンクチュアリになっており、その近辺にシジュウカラもいた。


有志の方が野鳥の写真も提供しているようだ。

池の脇にはちょっとした水生植物園もあり、睡蓮(ヒツジグサ)の花も見られて、とてもよい。

超望遠を買ったらまたゴイサギを撮りに来ようと思う。
How to Weight Edges with Number of Common Acquaintances
※ This article is translated version of 共通の知人数でエッジを重み付けする - SNAGeek
Introduction : the concept of "structural embeddedness"
The concept of structural embeddedness refers to how a certain tie is embedded in the social structure. This is measured by "how many common acquaintances exist between the two nodes."
The degree of structural embeddedness can be used as strength of a tie, when it is not possible to directly observe the depth of the relationship between node pairs, such as attachment or number of interactions. The structural features of the network are convoluted as edge weights.
The research that dealt with this, classically, has the following papers. In this paper, it is revealed that the number of common acquaintances is more time stable than the likes and dislikes and the time spent.
This concept is derived from Granovetter's "social embeddedness" concept. This is a concept that covers the type of ties and social situations such as "family relations" and "marital relations", but structural embeddedness focuses on structural aspects, especially.
The problem is how to calculate the number of people in common. You can implement it by the double loop, but if you exploit of the properties of the adjacency matrix, you can reduce it into matrix calculation, so it is possible to calculate very fast.
For undirected graphs without loops, if you calculate the power of the adjacency matrix, each element of the matrix is equal to the number of n-paths between i and j . When n = 2, the number of n-paths is the same as the number of nodes to which node i and node j are connected in common.
Implementation
Load libraries
library(igraph) library(ggnetwork) library(tidyverse)
Generate a random graph and visualize it
set.seed(111) network <- erdos.renyi.game(15,0.3) original_layout <- layout.fruchterman.reingold(network) gnet <- ggnetwork(network,layout = original_layout) g <- ggplot(gnet,aes(x=x,y=y,xend=xend,yend=yend)) g <- g + geom_edges(size=0.5) g <- g + geom_nodes(size=3) g <- g + geom_nodelabel(aes(label = vertex.names)) g <- g + theme_blank() g <- g + ggtitle("ORIGINAL NETWORK") g

The original adjacency matrix
adjmat <- as_adjacency_matrix(network) adjmat
15 x 15 sparse Matrix of class "dgCMatrix"
[1,] . . 1 . . . . . . 1 1 1 . . .
[2,] . . . . . . . . . . . . 1 1 1
[3,] 1 . . 1 1 . . . . 1 . 1 1 1 1
[4,] . . 1 . . . . . . . . . . 1 .
[5,] . . 1 . . . 1 . . . 1 . 1 . .
[6,] . . . . . . . 1 1 . . 1 1 . .
[7,] . . . . 1 . . 1 . . . . . . .
[8,] . . . . . 1 1 . 1 . . . . . .
[9,] . . . . . 1 . 1 . . 1 1 . 1 1
[10,] 1 . 1 . . . . . . . 1 . . 1 .
[11,] 1 . . . 1 . . . 1 1 . . . . 1
[12,] 1 . 1 . . 1 . . 1 . . . . . .
[13,] . 1 1 . 1 1 . . . . . . . . .
[14,] . 1 1 1 . . . . 1 1 . . . . .
[15,] . 1 1 . . . . . 1 . 1 . . . .
Next, let's square the adjacency matrix. To calculate matrix product in R, you can use %*% operator.
squared_adjmat <- adjmat %*% adjmat squared_adjmat
15 x 15 sparse Matrix of class "dgCMatrix"
[1,] 4 . 2 1 2 1 . . 2 2 1 1 1 2 2
[2,] . 3 3 1 1 1 . . 2 1 1 . . . .
[3,] 2 3 8 1 1 2 1 . 3 2 4 1 1 2 .
[4,] 1 1 1 2 1 . . . 1 2 . 1 1 1 1
[5,] 2 1 1 1 4 1 . 1 1 2 . 1 1 1 2
[6,] 1 1 2 . 1 4 1 1 2 . 1 1 . 1 1
[7,] . . 1 . . 1 2 . 1 . 1 . 1 . .
[8,] . . . . 1 1 . 3 1 . 1 2 1 1 1
[9,] 2 2 3 1 1 2 1 1 6 2 1 1 1 . 1
[10,] 2 1 2 2 2 . . . 2 4 1 2 1 1 2
[11,] 1 1 4 . . 1 1 1 1 1 5 2 1 2 1
[12,] 1 . 1 1 1 1 . 2 1 2 2 4 2 2 2
[13,] 1 . 1 1 1 . 1 1 1 1 1 2 4 2 2
[14,] 2 . 2 1 1 1 . 1 . 1 2 2 2 5 3
[15,] 2 . . 1 2 1 . 1 1 2 1 2 2 3 4
The elements of resulting matrix equal to the number of 2-paths for each component between i and j. Of course, the diagonal is equal to the degree of each node.
Finally, to weight only edges where there was an edge originally, calculate the element product with the adjacency matrix and finally calculate the element sum with the adjacency matrix.
weighted_adjmat <- squared_adjmat * adjmat + adjmat weighted_adjmat
> weighted_adjmat
15 x 15 sparse Matrix of class "dgCMatrix"
[1,] . . 3 . . . . . . 3 2 2 . . .
[2,] . . . . . . . . . . . . 1 1 1
[3,] 3 . . 2 2 . . . . 3 . 2 2 3 1
[4,] . . 2 . . . . . . . . . . 2 .
[5,] . . 2 . . . 1 . . . 1 . 2 . .
[6,] . . . . . . . 2 3 . . 2 1 . .
[7,] . . . . 1 . . 1 . . . . . . .
[8,] . . . . . 2 1 . 2 . . . . . .
[9,] . . . . . 3 . 2 . . 2 2 . 1 2
[10,] 3 . 3 . . . . . . . 2 . . 2 .
[11,] 2 . . . 1 . . . 2 2 . . . . 2
[12,] 2 . 2 . . 2 . . 2 . . . . . .
[13,] . 1 2 . 2 1 . . . . . . . . .
[14,] . 1 3 2 . . . . 1 2 . . . . .
[15,] . 1 1 . . . . . 2 . 2 . . . .
Let's visualize the weighted adjacency matrix. After creating a network object in igraph, subtract 1 from the edge weight. Edges that do not have any common acquaintances will be displayed with a weight of 0.
weighted_network <- graph.adjacency(weighted_adjmat, mode = "undirected", diag = FALSE, weighted = TRUE) E(weighted_network)$weight <- E(weighted_network)$weight - 1 gnet <- ggnetwork(weighted_network,layout = original_layout) g <- ggplot(gnet,aes(x=x,y=y,xend=xend,yend=yend)) g <- g + geom_edges(size=0.5) g <- g + geom_nodelabel(aes(label=vertex.names)) g <- g + geom_edgelabel(aes(label=weight)) g <- g + theme_blank() g <- g + ggtitle("WEIGHTED NETWORK") g



