このエントリは、Sansan Advent Calendar 2019 21日目の記事です。

基本的にタイトルの通りですが、この記事では統計的ネットワーク分析のデファクトスタンダードとなっているERGMをRで実装していきます。
- {igraph}以外のパッケージは使わずにできるだけスクラッチで開発します。
前もって断っておきますが、正しくパラメータ推定できるような実装には至ることができませんでした。

ERGMとは

ERGM = Exponential Random Graph Model
- 日本語では「指数ランダムグラフモデル」と訳されることが多いです。
- 略称は「あーぐむ」と読むようです。
概要については以下の記事で紹介されています。

qiita.com

ERGMを使うと何が嬉しいのか

観測されたネットワークが、どのような構造的なメカニズムによって生成されたのかを知ることができます。
ERGMの最大の強みは、ダイアド間の相互依存性を考慮できることにあります。
- ダイアドを1つのケースとして、エッジの有無を従属変数としたロジスティック回帰も可能ですが、これは残差の独立性の仮定に反してしまいます。
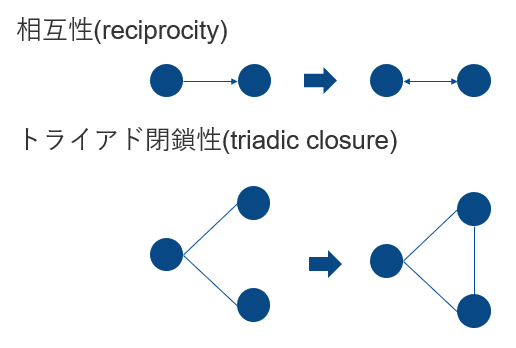
社会ネットワークにおいては、下の図のように、相互的なつながりが発生する傾向（相互性）や、友達同士は友達になりやすい傾向（トライアド閉鎖）がありますが、ERGMはダイアド同士の相互依存性を仮定できるので、このようなネットワーク内生的な効果を推定することができます。
- 例えば、トライアド閉鎖は、トライアングルの数などのネットワーク統計量をモデルに投入して、その効果を確認することができます。

f:id:meana0:20191220140649p:plain

ERGMは一般に以下のような指数形式で定式化されます。

$\displaystyle \Pr(\bf{Y}=\bf{y}) = \frac{1}{\kappa(\bf{y})} \exp\{\sum_A \theta_k g_k (\bf{y})\}$

$\displaystyle \kappa(\bf{y}) = \sum_{y' \in {Y}} \exp\{\theta^T g(y')\}.$

$\bf {Y}$ : ネットワークの確率変数。
$\bf {y}$ : ネットワークの実現値（実際に観測されたネットワーク）。
: ネットワーク形象のネットワーク統計量。
- 例えば、 $y$ に4つのトライアングルが含まれている場合、 $g_ {triangle}(\bf{k})= 4$ 。
$\theta_k$ : ネットワーク形象 $k$ に対応するパラメータ。
$A$ :モデル内で検討するトライアングルなどのネットワーク形象の集合。
$\kappa(\bf{y})$ : 正規化定数。可能なすべてのネットワークの $\exp{\theta_k g_k(y)}$ の合計値。
- N=20ほどの小規模ネットワークでも現実的に計算できない数の膨大なネットワークを検討しなければならないため、 $\kappa(\bf{y})$ の計算を回避するためのテクニックが色々と考案されています。
例えば、ERGMで以下のようにパラメータが推定されたとします。

Pr=exp(-0.5*エッジ数+0.5*閉鎖トライアドの数+0.2*同じ性別間のつながりの数)

この時、観測されたネットワークにおいて「友達同士が友達になりやすい」(トライアド閉鎖)という傾向と「同じ性別同士でつながりやすい」(ホモフィリー)という傾向が同時に作用していると解釈することができます。
ERGMを用いた研究事例は色々あるのですが、Goodreau et al. (2009)は、アメリカの学校内でのホモフィリーを、トライアド閉鎖の効果を統制しながら推定しています。

www.ncbi.nlm.nih.gov

ここからは、{ergm}パッケージを用いたERGMの推定と、RによるERGMパラメータ推定の実装の一例について紹介します。

セッション情報

RStudio Cloud上で動かしています。

> sessionInfo()
R version 3.5.3 (2019-03-11)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 16.04.6 LTS

Matrix products: default
BLAS: /usr/lib/atlas-base/atlas/libblas.so.3.0
LAPACK: /usr/lib/atlas-base/atlas/liblapack.so.3.0

locale:
 [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8        LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8   
 [6] LC_MESSAGES=C.UTF-8    LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C           LC_TELEPHONE=C        
[11] LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] coda_0.19-2           forcats_0.3.0         stringr_1.3.1         dplyr_0.8.3           purrr_0.3.3          
 [6] readr_1.3.1           tidyr_0.8.2           tibble_2.1.3          ggplot2_3.1.0         tidyverse_1.2.1      
[11] igraph_1.2.4.1        statnet_2019.6        tsna_0.3.0            sna_2.4               ergm.count_3.3.0     
[16] statnet.common_4.3.0  tergm_3.6.1           networkDynamic_0.10.0 ergm_3.10.4           network_1.15

{ergm}の使い方

github.com

アメリカ西海岸のネットワーク分析の研究者らが中心となって開発されているパッケージです。
社会ネットワーク分析用の{sna}やネットワークオブジェクトを管理する{network}などが全部入りの{statnet}というパッケージスイートがあり、こちらを導入するのが便利です。

> library(statnet)
statnet: version 2019.6, created on 2019-06-13
Copyright (c) 2019, Mark S. Handcock, University of California -- Los Angeles
                    David R. Hunter, Penn State University
                    Carter T. Butts, University of California -- Irvine
                    Steven M. Goodreau, University of Washington
                    Pavel N. Krivitsky, University of Wollongong
                    Skye Bender-deMoll
                    Martina Morris, University of Washington
Based on "statnet" project software (statnet.org).
For license and citation information see statnet.org/attribution
or type citation("statnet").

今回は、メディチ家の婚姻ネットワークデータ flomarriage を用います。
とりあえず plot してみます。

data(florentine)
plot(flomarriage)

f:id:meana0:20191219230711p:plain

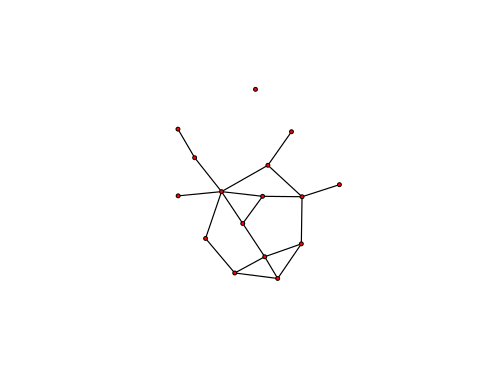
ネットワーク統計量は summary() 関数を使うと計算できます。
- 今回は、エッジの本数(edges)とトライアングル(triangle)に着目します。

> summary(flomarriage ~ edges + triangle)
   edges triangle 
      20        3

これらのネットワーク統計量からなるモデルを構築し、ERGMのパラメータを推定してみます。

> ergm_model <- ergm(flomarriage ~ edges + triangle)
Starting maximum pseudolikelihood estimation (MPLE):
Evaluating the predictor and response matrix.
Maximizing the pseudolikelihood.
Finished MPLE.
Starting Monte Carlo maximum likelihood estimation (MCMLE):
Iteration 1 of at most 20:
Optimizing with step length 1.
The log-likelihood improved by 0.003736.
Step length converged once. Increasing MCMC sample size.
Iteration 2 of at most 20:
Optimizing with step length 1.
The log-likelihood improved by 0.0002205.
Step length converged twice. Stopping.
Finished MCMLE.
Evaluating log-likelihood at the estimate. Using 20 bridges: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 .
This model was fit using MCMC.  To examine model diagnostics and check
for degeneracy, use the mcmc.diagnostics() function.

結果を確認してみます。通常の lm と同じく、summary() 関数で推定結果の詳細を確認できます。

>summary(ergm_model)
==========================
Summary of model fit
==========================

Formula:   flomarriage ~ edges + triangle

Iterations:  2 out of 20 

Monte Carlo MLE Results:
         Estimate Std. Error MCMC % z value Pr(>|z|)    
edges     -1.6743     0.3488      0  -4.801   <1e-04 ***
triangle   0.1626     0.5894      0   0.276    0.783    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

     Null Deviance: 166.4  on 120  degrees of freedom
 Residual Deviance: 108.1  on 118  degrees of freedom
 
AIC: 112.1    BIC: 117.6    (Smaller is better.)

実装編

さて、続いてはRでできるだけゼロからERGMを実装することを試みます。

下準備

flomarriageは network オブジェクトなので、 igraph オブジェクトに変換します。
- {intergraph} を用いると、この作業が非常に簡単になります。

library(igraph)
library(intergraph)
g <- intergraph::asIgraph(flomarriage)
plot(g)

f:id:meana0:20191219233118p:plain

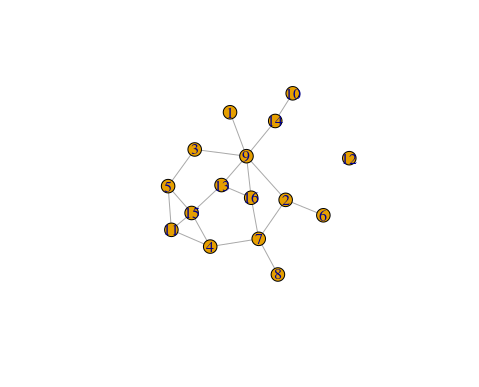
ネットワーク統計量を計算する関数

本当は行列計算でも書けるのですが…

#エッジの数
count_edges <- function(g){
  edges <- length(E(g))
  return(edges)
}

#トライアングルの数
count_triangle <- function(g){
  triangle <- motifs(g)[4]
  if(is.na(triangle)){
    triangle <- 0
  }
  return(triangle)
}

先ほどの結果と一致します。

> count_edges(g)
[1] 20
> count_triangle(g)
[1] 3

推定のステップ

ERGMのパラメータ推定は以下のステップで行われます。

(1) 疑似尤度最大化(MPLE)による $\theta_0$ の決定

(2) MCMCによるランダムグラフ生成

(3) (2)で得られたサンプルを用いた対数尤度比の最大化 -> $\hat{\theta}$ の推定

(2),(3)のステップはモンテカルロ尤度最大化(MC-MLE)と呼ばれています。
少しトリッキーになりますが、MC-MLEの説明から始めます。

変化統計量

MC-MLE自体の説明に入る前に、まず、変化統計量について説明します。
他のすべてのダイアドの状態 $y_{ij}^c$ を一定として、ダイアド $ij$ の状態を変化させた時の、ネットワーク統計量の変化を 変化統計量(change statistics)と呼びます。

$\displaystyle \Delta g(y)_{ij} = g(y^+)_{ij} - g(y^-)_{ij}$

MCMCによるランダムグラフ生成

ある固定された $\theta_0$ のもとで、変化統計量の比 [\pi] を計算します。
$\theta_0$ を上手く決めれば、観測されたネットワークに近いようなランダムグラフが生成されていきます。

$\displaystyle \pi = \frac{ \Pr(Y_{ij}\,changed \ |\ Y_{ij}^c = y_{ij}^c ) }{ \Pr(Y_{ij}\,not\,changed \ |\ Y_{ij}^c = y_{ij}^c ) } = \theta_0^T\ [\pm \Delta g(y)_{ij} ]$

$\min(1,\pi)$ を遷移確率として、次のサンプルに進みます。こうしてランダムグラフのサンプルを生成していきます。

##ダイアドの状態をスイッチさせる
change_edge <- function(graph,i,j){
  if(graph[i,j] == 1){
    graph[i,j] <- 0
  }else{
    graph[i,j] <- 1
  }
  return(graph)
}

##ランダムにダイアドの状態をスイッチさせたグラフを返す
random_propose <- function(graph){
  sampled_pairs <- sample(1:length(V(graph)),2,replace = FALSE)
  i <- sampled_pairs[1]
  j <- sampled_pairs[2]
  graph <- change_edge(graph,i,j)
  return(graph)
}

MC-MLE

メトロポリス-ヘイスティングス法の実装

metropolis <- function(graph, theta0_edges, theta0_triangle){
  
  ##現在のネットワーク
  current_graph <- graph
  current_edges <- count_edges(current_graph)
  current_triangle <- count_triangle(current_graph)
  
  ##提案されたネットワーク
  proposed_graph <- random_propose(graph)
  proposed_edges <- count_edges(proposed_graph)
  proposed_triangle <- count_triangle(proposed_graph)
  
  ##変化統計量の計算
  changed_edges <- proposed_edges - current_edges
  changed_triangle <- proposed_triangle - current_triangle
  
  ##piを計算し、提案されたグラフを採択するかどうか決める
  change_ratio <- exp(theta0_edges*changed_edges + theta0_triangle*changed_triangle)
  move_probability <- min(1,change_ratio)
  if(move_probability >= runif(1)){
    return(proposed_graph)
  }else{
    return(current_graph)
  }
}

MCMCの実装

MCMC <- function(graph, burn_in = 10000, samplesize = 50000, theta0_edges = 0.1, theta0_triangle = 0.1){
  graph <- graph.empty(length(V(graph)),directed=FALSE)
  edges_c <- count_edges(graph)
  triangle_c <- count_triangle(graph)
  par(mfrow = c(2,2))
  for(i in 1:samplesize){
    if(i %% 1000 == 0){
      progress_text <- paste0(i,"(",round(100*(i/samplesize),3),"%) done")
      print(progress_text)
      plot(edges_c,type="l")
      hist(edges_c)
      plot(triangle_c,type="l")
      hist(triangle_c)
    }
    after_graph <- metropolis(graph,theta0_edges,theta0_triangle)
    edges_c <- c(edges_c,count_edges(after_graph))
    triangle_c <- c(triangle_c,count_triangle(after_graph))
    graph <- after_graph
  }
  return(list(edges = edges_c[(burn_in+1):samplesize], triangle = triangle_c[(burn_in+1):samplesize],obs_graph = graph))
}

MPLE

さて、ここまでMCMCを用いたランダムグラフの生成は $\theta _ 0$ を前提としていましたが、この値自体はどのように決めればいいのでしょうか。
実は、 $\theta _ 0$ は $\theta$ の真値に近くないと、正しい分布からランダムグラフを生成してくれないという問題があるため、できるだけ近い値を $\theta _ 0$ としたいです。
そこで、疑似尤度の最大化(Maximum Pseudo-Likelihood Estimation, MPLE)で推定されたパラメータをとします。
- これは、ダイアド同士の統計的連関を考慮しないモデル (dyad-independence) と同値であり、構造的特徴のないモデルではMCMCを行わず、MPLEのみが使われます。
これは非常にシンプルで、観測されたネットワークのダイアドにおけるエッジの有無を、ネットワーク統計量の変化統計量で回帰するロジスティック回帰を行うことで達成されます。

#変化統計量とエッジの存在からなるデータフレームを生成
generate_changed_data <- function(graph){
  changed_data <- data.frame()
  for(i in 1:length(V(graph))){
    for(j in 1:length(V(graph))){
      if(i >= j){
        next
      }
      existing_if <- graph[i,j]
      changed_graph <- change_edge(graph,i,j)
      changed_triangle <- abs(count_triangle(changed_graph) - count_triangle(graph))
      row <- data.frame(i = i, j = j, existing_if = existing_if, changed_triangle = changed_triangle)
      changed_data <- rbind(changed_data,row)
    }
  }
  return(changed_data)
}

#MPLEの実装
MPLE <- function(graph){
  data_for_mple <- generate_changed_data(graph)
  reg <- glm(data = data_for_mple, existing_if ~ changed_triangle, family = "binomial")
  return(list(edges = reg$coefficients["(Intercept)"], triangle = reg$coefficients["changed_triangle"]))
}

MPLE -> MC-MLEまでのプロセス

## SAMPLING
triangle_model <- function(graph, burn_in = 10000, samplesize = 50000){
  message("Starting MPLE fitting...")
  theta0_list <- MPLE(graph)
  print(theta0_list)
  message("MPLE fitting done. Now starting MC-MLE fitting...")
  fit <- MCMC(graph,
              burn_in = burn_in,
              samplesize = samplesize,
              theta0_edges = theta0_list$edges,
              theta0_triangle = theta0_list$triangle)
  fit$theta0_edges <- theta0_list$edges
  fit$theta0_triangle <- theta0_list$triangle
  return(fit)
}

実際にMCMCからネットワーク統計量のサンプルを得ます。

fit <- triangle_model(g, burn_in = 10000, samplesize = 50000)

対数尤度比の最大化

さて、MCMCからネットワーク統計量のサンプルが得られました。次はこれを用いて、実際にパラメータを推定していきます。
尤度それ自体は正規化定数を計算しなければ最大化できないので、代わりに、ある固定された $\theta_0$ を用いた $\ell(\theta)-\ell(\theta_0)$ =対数尤度比の最大化を目指します。
は、以下のように近似できます。
- $m$ : MCMCで得られたランダムグラフで、近似に用いる数。
- $y_i$ : MCMCで得られたランダムグラフで、近似に用いる $i$ 番目のサンプル。

$\displaystyle \ell(\theta)-\ell(\theta_0) \approx (\theta - \theta_0)^T g(y) - \log[ \frac{1}{m}\sum_{i=1}^m \exp\{ (\theta-\theta_0)^T g(y_i) \} ]$

#対数尤度比を計算する関数
loglikelihood_ratio <- function(theta,fit,n){
  sample_length <- length(fit$edges)
  sample_index <- (sample_length-n):sample_length
  sampled_edge_count <- fit$edges[sample_index]
  sampled_triangle_count <- fit$triangle[sample_index]
  theta0 <- c(fit$theta0_edges,fit$theta0_triangle)
  g_obs <- c(count_edges(fit$obs_graph),count_triangle(fit$obs_graph))
  first = (theta - theta0) %*% g_obs
  exp_vec <- c()
  for(i in 1:n){
    sam <- exp((theta - theta0) %*% c(sampled_edge_count[i],sampled_triangle_count[i]))
    exp_vec <- c(exp_vec,sam)
  }
  second <- log(sum(exp_vec)/length(exp_vec))
  loglikelihood_ratio <- first - second
  return(loglikelihood_ratio)
}

optim() 関数を使って、MCMCで得られたグラフのネットワーク特徴を与えて、対数尤度比を最大化してみます。

##対数尤度比の最大化
my_estimates <- optim(par = c(0,0), #初期値
                      fn = loglikelihood_ratio, #目的関数
                      control = list(fnscale=-1), #最大化するため
                      fit = fit,
                      n = 1000) #MCMCサンプルサイズ

さて、いよいよオレオレERGMの推定結果を確認します。
{ergm}で求めたパラメータと比べてみます。

> ergm_model$coef #推定結果 ({ergm})
    edges  triangle 
-1.674332  0.162630 
> my_estimates$par #推定結果 (オレオレergm)
[1] -1.8267176  0.2983575

それなりに近い推定値にはなっているものの、ややズレてしまっています。

問題：MCMCが上手くランダムグラフを生成していない

当初は最適化関数の扱いに問題があるのかと思い、初期値などを色々試してみるも無駄に終わってしまいました。
調べてみると、MCMCが上手くランダムグラフを生成していまいことがわかりました。
まず、{ergm}を用いて生成したmcmcsampleは以下のようなtraceplotを呈します。
- わかりやすくするために、観測されたグラフのネットワーク統計量が0になるようにセンタリングしています。

> mcmc.diagnostics(ergm_model, esteq = FALSE, center = TRUE)

f:id:meana0:20191219235557p:plain

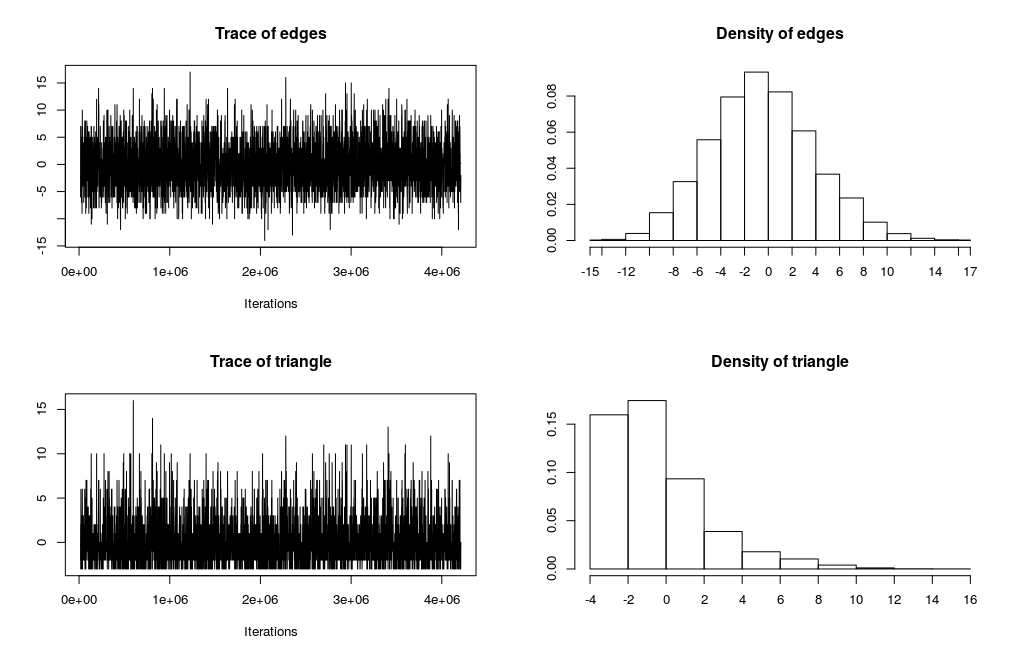
一方、自分で実装したmcmcsampleを見てみます。
ergm::mcmc.diagnostics() と似たプロットを行う関数を作ります。

##オレオレMCMCのサンプル生成結果をplot
diagnosis <- function(fit){
  edges_c <- fit$edges
  triangle_c <- fit$triangle
  obs_edges <- count_edges(fit$obs_graph)
  obs_triangle <- count_triangle(fit$obs_graph)
  edges_centered <- edges_c - obs_edges
  triangle_centered <- triangle_c - obs_triangle
  par(mfrow = c(2,2))
  plot(edges_centered,type="l",)
  hist(edges_centered)
  plot(triangle_centered,type="l")
  hist(triangle_centered)
}

結果がこちらです。

> diagnosis(fit)

f:id:meana0:20191220000006p:plain

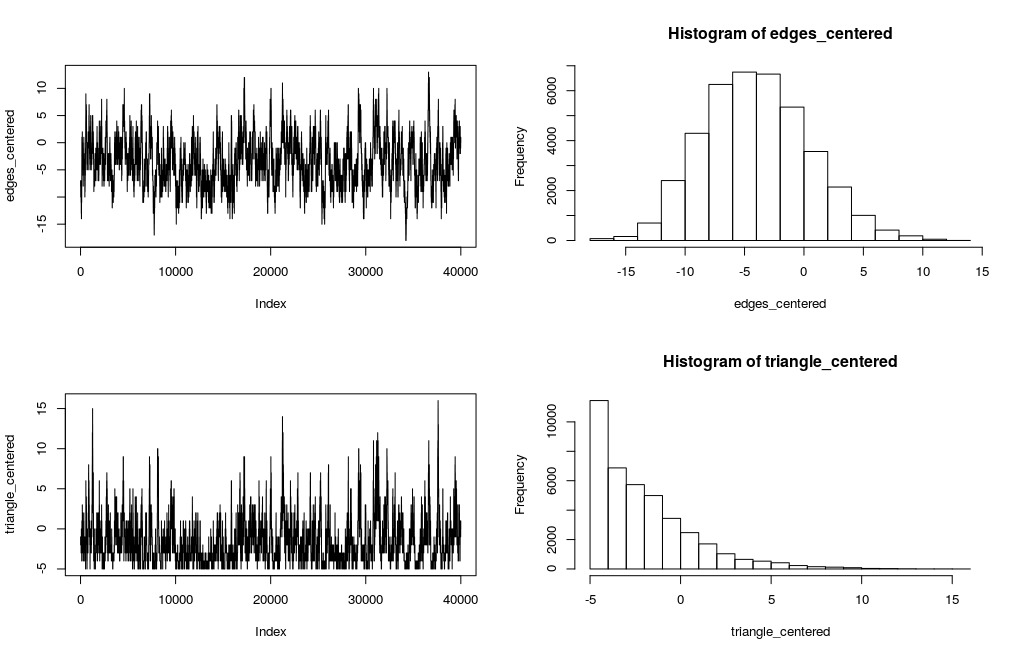
観測値に比べるとマイナス側に偏った分布になってしまっています。

さいごに

今回は時間が足りず、これ以上のことはできませんでした。
尻切れトンボにようになってしまいますが、なぜ上手く推定できないのかも含めて、この課題に引き続き取り組んでいこうと思います。

参考文献

Garry RobinsらによるERGMの総説論文：An introduction to exponential random graph (p*) models for social networks - ScienceDirect
ERGMの推定法に関するコンパクトなまとめ：Archive ouverte HAL - Introduction to network modeling using Exponential Random Graph models (ERGM)
statnetチームによる過去のワークショップ資料：https://statnet.org/trac/wiki/WorkshopArchive
- 推定に関して一番わかりやすいのはHunterによる2006年のEstimationの資料
ERGMs with Rhttps://acaimo.github.io/SNAR_BOOK/MLE-ERGMs.html#monte-carlo-maximum-likelihood-estimation-mc-mle

SNAGeek

Sociologically Technological, and Technologically Sociological

RでERGMを実装したかった（が、失敗した）